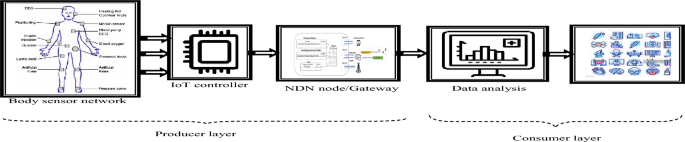
Optimal Key Generation
In the recommended architecture, key extraction plays a key role in both the recovery and sanitization operations, where optimizations are performed with the support of the designed RPCSO algorithm. Answer conversion is an early stage in the development of the key. At this time, the key is \(ky\) It is transformed into another form with the help of the “Kronecker” approach, after which the key is changed to: \(ky_{1}\) Using equation (5), the magnitude is taken as follows: \(\sqrt {no^{\prime\prime}} \times Q_{\max }\)For example, the key matrix is created and given by equation (5) for the key. \(= \left\{ {9,8,3} \right\}\).
$$ky_{1} = \left( {\begin{array}{*{20}c} 9 & 9 & 9 \\ 8 & 8 & 8 \\ 3 & 3 & 3 \\ \end{array} } \right)_{{\left( {\sqrt {no^{\prime\prime}} \times q_{\max } } \right)}}$$
(5)
variable \(no\) Shown as transaction number and coefficient \(No^{\prime\prime}\) is expressed as the “nearest perfect square of the number”. Furthermore, the variable \(Q_{\max}\) is It is specified as the longest transaction length. According to formula (6), the reconstructed key matrix \(ky_{1}\) It is generated by processing row-wise duplication. Also, the key matrix \(ky_{2}\) is developed with the support of the “Nonecker” approach and is formulated in Eq. (6).
$$ky_{2} = ky_{1} \otimes ky_{1}$$
(6)
The “Kronecker” product can be expressed as follows: \(\otimes\) And size \(ky_{2}\) can also be written as: \(\sqrt {no^{\prime\prime}} \times Q_{\max }\)Here, the main goal of the proposed task is key optimization utilizing the proposed RPCSO algorithm. The optimal key construction task utilizing the proposed RPCSO is shown in Figure 4.
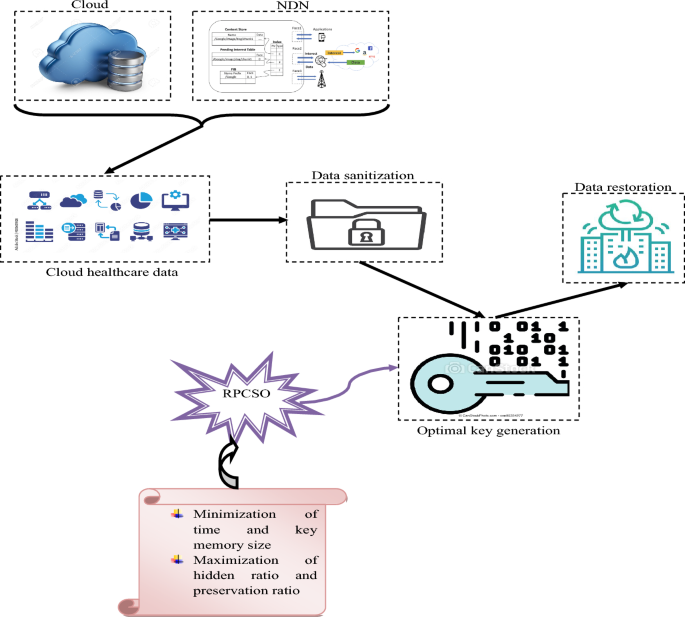
RPCSO-based optimal key generation task.
Proposal of an architecture process with different layers of NDN
In the proposed framework, the system is classified into IoT system, user system, and edge system. The IoT system 26 is divided into cluster candidates responsible for monitoring and obtaining healthcare information, and cluster heads responsible for collecting healthcare information from members of the cluster. Every sick person is assigned different cluster candidates and cluster heads that can be built on the fabric belt. Based on the category of the system, the framework includes a user layer, an edge cloud layer, and a patient layer. The patient layer includes cluster candidates, and the cluster heads periodically collect the healthcare data detected by the cluster candidates. Then, the collected information is transferred to the edge cloud for catching. The edge cloud layer is then integrated with the edge system that provides a computation and storage system to quickly catch and provide the healthcare information. Furthermore, the user layer includes user systems such as computers that leverage the benefits of NDN to realize safe and effective healthcare information retrieval. According to the hierarchical layers, a framework for hierarchical medical monitoring is recommended. In this task, the work includes a prefix indicating the medical sector, such as a hospital, the patient is introduced by the patient IOD, and the category of medical data, such as blood pressure, is detected by the medical data ID. Prefixes are supported to describe each system.,The downstream interfaces of edge systems are connected to,user systems or cluster heads, and edge systems are linked by,upstream interfaces.,For IoT-assisted devices, an attacker needs to,consider several features.
1.
It reads and receives all network traffic.
2.
Distributes network traffic.
3.
Sends and forges network traffic.
Depending on their capabilities, attackers can deploy multiple threats, including spoofing and eavesdropping.Since the encryption and hashing approach can convert plaintext into ciphertext, experts have utilized the proposed architecture to achieve security for data distribution in the medical field. \(Y\) Prefix, \(y^{th}\) Prefix \(Px_{y} \,\,\,\left( {1 \le y \le Y} \right)\) Next, a “Trusted Authority (TA)” creates a shared key. \(K_{y}\) Provide a one-way hash function \(H_{y}\)This is derived from equation (7).
$$K_{y} = KG\left( {Px_{y} , master key} \right)$$
(7)
This term \(Px_{y}\) Hash Prefix \(HPx_{y}\) is formulated as equation (8).
$$HPx_{y} = H_{y} \left( {Px_{y} ,K_{y} } \right)$$
(8)
For edge systems \(Es_{y}\) Estimated by variables \(Px_{y}\) And it is provided with factors \(HPx_{y}\)Patient registry \(Z\) Healthcare organizations and \(HI_{yz}\) Considered by variables \(Px_{y}\),after that, \(z^{th}\) Patient \(Pa_{yz} \,\,\,\left( {1 \le z \le Z} \right)\) A typical TA creates a shared key \(K_{yz}\) Provide a one-way hash function \(H_{yz}\)This is expressed by equation (9).
$$K_{yz} = KG\left( {Pa_{yz} ,Master Key} \right)$$
(9)
All Healthcare Data \(MD_{yza}\) Variable \(Pa_{yz}\),factor \(MD_{yza}\) Judging from the name \(Na_{Iza}\) Here the variable \(Px_{y}\) is represented as a prefix. And the patient’s ID is \(SID_{y}\) Healthcare information IDs are specified as follows: \(HID_{z}\)the variables are pointed to as follows: \(HPID_{yz}\) Variable Hash Patient ID \(SID_{y}\)This is shown in equation (10). Also, the ID of the hashed medical data is shown as follows: \(HMID_{yza}\) variable \(HID_{a}\) This is derived from equation (11).
$$HPID_{yz} = H_{yz} \left( {SID_{z} ,K_{zy} } \right)$$
(10)
$$HMID_{yza} = H_{yz} \left( {MID_{z} ,K_{zy} } \right)$$
(11)
Hash Name \(HNa_{yza}\) Variable \(Na_{Iza}\) is expressed as follows: \(HPx_{y} /HSID_{yz} /HMID_{yza}\) And the cause \(MD_{yza}\) Encrypted medical information \(EMD_{yza}\) is formulated in Equation (12). Once authorized candidates such as doctors have legal access, \(MD_{yza}\) And he \(K_{yz} \,\,\,\,and\,\,\,\,HNa_{yza}\)Furthermore, all legitimate edge and IoT systems are built using private and public keys.
$$EMD_{yza} = Encryption\left( {MD_{yza} ,K_{yz} } \right)$$
(12)
Data sanitization is an operation that hides sensitive information or data, which helps to prevent data from being exposed to illegal users, and restoration is the inverse operation of the data sanitization task that is performed to estimate the effectiveness of the sanitization task. During the data sanitization task, a binary transformation is performed for the creation of both the key matrix and the data. The suggested RPCSO algorithm is used to create the optimal key. The proposed “NDN-based Edge Computing in IoT-enabled Healthcare Systems” architecture is shown in Figure 5.
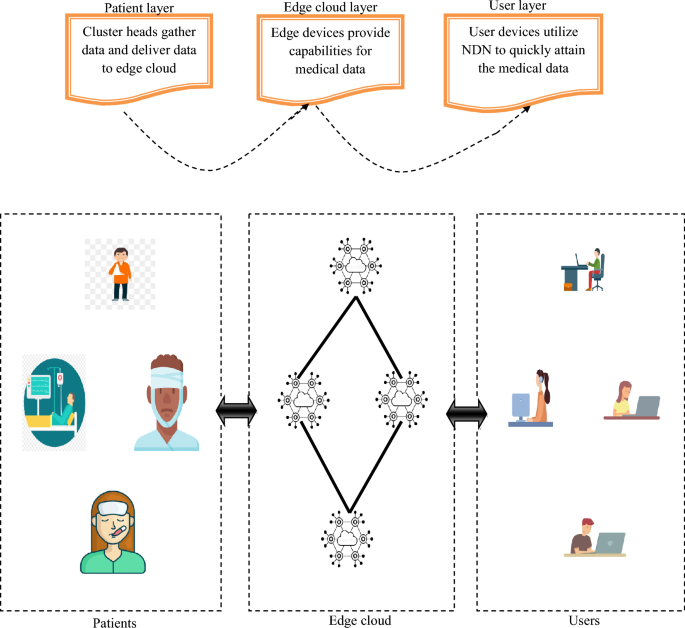
A recommended NDN-based edge computing architecture for IoT-enabled healthcare systems.
The main goal of this task is to implement a secure architecture for edge computing in IoT-assisted medical model by utilizing heuristic-assisted authentication and NDN. The proposed task has three layers: patient layer, edge cloud layer, and user layer. In the first layer, various IoT systems are linked and utilizing cluster head data, patients transfer their information to the edge cloud layer. The edge cloud layer is responsible for computing and storage assets to quickly serve and cache medical information. Thus, the patient layer is an advanced heuristic-assisted sanitization approach called RPCSO with NDN to conceal sensitive information that should not be exposed to unauthorized candidates. The authentication approach utilizes a multi-objective function key development task on factors such as change degree, preservation rate, and concealment failure rate. Furthermore, the information from the edge cloud layer is sent to the user layer, where the generation of optimal keys with NDN-assisted recovery is processed to achieve secure and effective medical data retrieval. The task is quantitatively evaluated based on multiple healthcare data sources from Kaggle and UCI repositories, and the research evaluation shows the superior functionality of the recommender system considering cost and latency when compared to traditional solutions.
Objective function and its constraint specification
The proposed NDN-based edge computing in IoT-enabled healthcare systems helps in data sanitization and restoration. Sanitization supports hiding data, and the restoration operation is the reverse operation of data sanitization. Data sanitization operation protects confidential information and reduces asset disposal. Moreover, the data restoration approach is cost-effective and simplified in management. However, data sanitization operation does not provide the location of hidden data and is very time-consuming. Similarly, data restoration task is very complicated and overall data restoration requires more safety management, storage space, and time. Therefore, the proposed NDN-based edge computing in IoT-enabled healthcare systems helps in providing more effective data sanitization and data restoration task. In this task, a binary format key is used to perform the task. This key is optimally tuned by the suggested RPCSO algorithm. First, the raw data is \(S_{d}\) is given as input and then the data is sanitized \(S_{d}^{san}\) With the support of the edge cloud layer, the sanitized data is then \(S_{d}^{san}\) To be restored \(S_{d}^{res}\) The user layer optimizes the key with the support of the optimal key. The objective function of key optimization is shown in Equation (13).
$$ob = \mathop {\arg \,\,\,\min }\limits_{{\left\{ {Ke_{g} } \right\}}} \left( {T + Ms + \frac{1 }{\Pr } + \frac{1}{Hr}} \right)$$
(13)
Here, the optimized key is expressed as: \(Ke_{g}\) This is in binary form, i.e. 0 or 1. Furthermore, the coefficient \(T\) Representing time and coefficients \(MS\) Specifies the memory size of the key. The storage rate and obscuration rate are expressed as follows: \(\Pr \,\,\,\,and\,\,\,\,\,\,Hr\) These constraints are explained as follows:
time \(T\) “That is the element that is estimated to complete the entire process.”
Key memory size \(MS\) “The goal is to see how much memory is used for the optimal key.”
Save Rate \(\Pr \,\) “This is the inverse of data loss and is expressed in equation (14).
$$\Pr \, = \frac{{I_{2} }}{TI}$$
(14)
Here, the variable \(I_{2}\) It points to the zero-indexed number, then \(TI\) It is expressed as the total amount of data indexes that will be stored.
Concealment \(Hr\,\) “It is the fraction by which the sensitive data is effectively hidden.” It is given by equation (15).
$$Hr\, = \frac{{I_{1} }}{TP}$$
(15)
This factor is \(I_{1}\) Specifies how much of the data index needs to be hidden, and the length of the non-zero index is \(TP\).